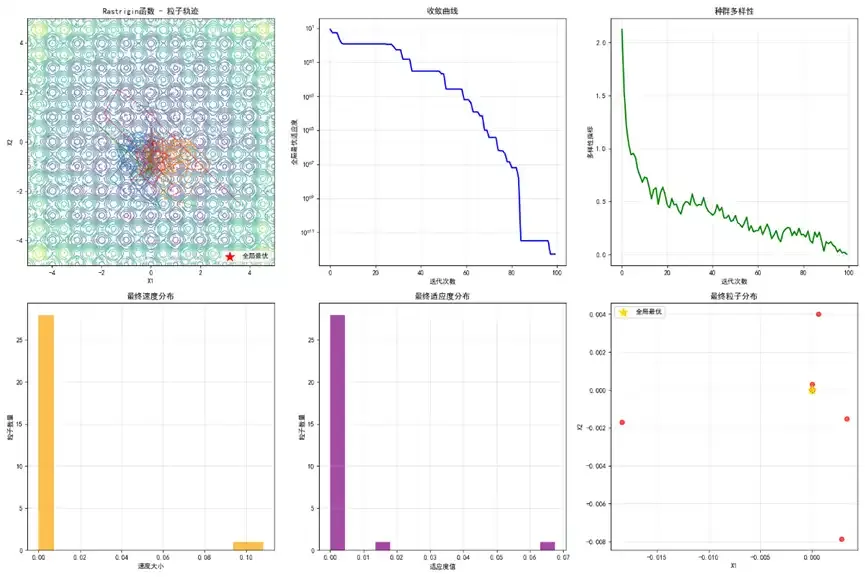
粒子群算法 • ArronHC的博客

粒子群算法（PSO）#

1.介绍#

以一群蜜蜂寻找最甜的花为例
- 他们很盲目：不知哪里最甜
- 有记忆：知道自己到过最甜的位置
- 有沟通：知道群体最甜的位置于是，对于每只蜜蜂，它下次飞行会综合考虑以下三个方面：
按照惯性，沿着上一次的方向再飞一会儿
自己的最甜处，即个体最优解(pbest, Personal Best)
群体的最甜处，即全局最优解(gbest, Global Best) 然后在迭代后，所有蜜蜂都会找到最甜处

2.算法讲解#

现在，我们把上面的故事翻译成算法的语言：

粒子 (Particle)：就是一只蜜蜂。在算法里，它代表一个潜在的解。
种群/粒子群 (Swarm)：就是整个蜂群。它是一组潜在的解。
位置 (Position, x)：就是蜜蜂所在的位置坐标。在算法里，它就是这个潜在解的具体数值。如果我们要优化函数 f(x, y)，那么一个粒子的位置就是 (x, y)。
速度 (Velocity, v)：就是蜜蜂飞行的方向和距离。它决定了粒子下一次移动的方向和步长。速度越大，粒子移动得越快、越远。
适应度 (Fitness)：就是蜜蜂闻到的花香浓度。在算法里，通常由一个目标函数（也叫适应度函数）来计算。我们的目标就是找到适应度最高（或最低）的位置。例如，寻找函数的最小值时，函数值就是适应度，越小越好。
个体最优解 (pbest, Personal Best)：就是某只蜜蜂自己历史上去过的最香的位置。每个粒子都有自己的 pbest。
全局最优解 (gbest, Global Best)：就是整个蜂群目前发现的最香的位置。所有粒子共享同一个 gbest。

3.算法流程#

Step1：初始化

随机一群粒子
为每个粒子随机分配参数（对于蜜蜂，就是初始位置 x 和初始速度 v）
计算每个粒子的适应度 (适应度函数就是目标函数)
将当前适应度设置为每个个体的 pbest
从所有 pbest 中选出 gbest Step2：迭代
步骤与 Step1 相同，每次迭代会更新每个粒子的 x 和 v，从而得到更好的 pbest 和 gbest

4.PSO 的灵魂：迭代函数#

速度更新公式：

v(t+1)=w*v(t)+c_1*rand_1*(pbest-x(t))+c_2*rand_2*(gbest-x(t))

其中，

$v(t+1)$ ：粒子下一刻速度
$w$ ：惯性权重
$c_1$ ：自我学习部分的学习因子
$rand_1$ ：0~1 的随机数
$c_2$ ：群体学习部分的学习因子
$rand_2$ ：0~1 的随机数
$c_1*rand_1*(pbest-x(t))$ 表示粒子向 pbest 飞行的趋势
$c_2*rand_2*(pbest-x(t))$ 表示粒子向 gbest 飞行的趋势

值得注意的是

在实际应用是，v, x 是多维的向量，每个维度就代表一个的参数

位置更新公式：

x(t+1)=x(t)+v(t+1)

5. 代码实战#

理论说完了，我们来点实际的。用 Python 实现 PSO，求解函数 f(x, y) = x² + y² 在 [-10, 10] 区间内的最小值。我们都知道，最小值在 (0, 0)，值为 0。看看 PSO 能不能找到它。

import numpy as np

# --- 1. 定义目标函数 (适应度函数) ---
def objective_function(position):
    # position 是一个包含 x 和 y 的数组/列表，例如 [x, y]
    return position[0]**2 + position[1]**2

# --- 2. PSO 参数设置 ---
w = 0.5         # 惯性权重
c1 = 1.5        # 个体学习因子
c2 = 1.5        # 社会学习因子
n_particles = 50 # 粒子数量
n_dimensions = 2 # 问题维度 (x, y)
max_iter = 100   # 最大迭代次数
bounds = [(-10, 10), (-10, 10)] # 搜索范围

# --- 3. 初始化粒子群 ---
# 初始化粒子位置
particles_pos = np.random.uniform(bounds[0][0], bounds[0][1], (n_particles, n_dimensions))
# 初始化粒子速度
particles_vel = np.random.rand(n_particles, n_dimensions)

# 初始化个体最优解 (pbest) 和其适应度
pbest_pos = particles_pos.copy()
pbest_fitness = np.array([objective_function(p) for p in pbest_pos])

# 初始化全局最优解 (gbest) 和其适应度
gbest_idx = np.argmin(pbest_fitness)
gbest_pos = pbest_pos[gbest_idx].copy()
gbest_fitness = pbest_fitness[gbest_idx]

# --- 4. 迭代优化 ---
print(f"开始优化，共 {max_iter} 代...")

for i in range(max_iter):
    for j in range(n_particles):
        # --- 更新速度 ---
        r1 = np.random.rand(n_dimensions)
        r2 = np.random.rand(n_dimensions)
        
        cognitive_vel = c1 * r1 * (pbest_pos[j] - particles_pos[j])
        social_vel = c2 * r2 * (gbest_pos - particles_pos[j])
        particles_vel[j] = w * particles_vel[j] + cognitive_vel + social_vel

        # --- 更新位置 ---
        particles_pos[j] = particles_pos[j] + particles_vel[j]
        
        # --- 边界处理 ---
        for k in range(n_dimensions):
            if particles_pos[j, k] < bounds[k][0]:
                particles_pos[j, k] = bounds[k][0]
            elif particles_pos[j, k] > bounds[k][1]:
                particles_pos[j, k] = bounds[k][1]

        current_fitness = objective_function(particles_pos[j])
        
        # --- 更新 pbest 和 gbest ---
        # 更新个体最优
        if current_fitness < pbest_fitness[j]:
            pbest_fitness[j] = current_fitness
            pbest_pos[j] = particles_pos[j].copy()

        # 更新全局最优
        if current_fitness < gbest_fitness:
            gbest_fitness = current_fitness
            gbest_pos = particles_pos[j].copy()

    # 每一代打印一次最优结果
    if (i + 1) % 10 == 0:
        print(f"第 {i+1} 代: 最优位置 = {gbest_pos}, 最优值 = {gbest_fitness:.6f}")

# --- 5. 输出最终结果 ---
print("\n优化结束!")
print(f"找到的最优位置 (gbest): {gbest_pos}")
print(f"找到的最优值: {gbest_fitness}")

python

你可以运行这段代码，会看到 gbest 的值随着迭代次数的增加，越来越接近 (0, 0)，最优值也越来越接近 0。